国考行测图形推理，“立体拼合”实用技巧
国家公务员考试行测判断推理考点累积 本文，小编给大家带来行测“立体拼合”的实用技巧，一起来学习：
判断推理例题讲解 1.题型判定：
提问：题干中完整图形是由残缺图形与哪个选项共同构成？
题干：给出一个完整图形及几个残缺图形（如下图所示）。
2.解题思路：
凹凸一致，有凹必有凸，有凸必有凹。具体要考虑两个方面：
（1）凹进去的部分与凸出来的部分形状相同，如上图中图2与图3可拼合为图1。
（2）凹进去的部分与凸出来的部分对应长度相同。
小贴士：
立体拼合题目可以先观察题干和选项的“凹凸”部分的形状，通常情况下可以排除1-2个错误选项，再对剩余选项拼合的部分进行长度上的比较。
真题示例1（2019联考）正方体切掉一块后剩余部分如下图左侧所示，右侧哪一项是其切去部分的形状？
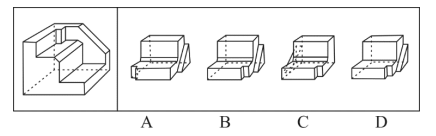
【题型判定】通过问题可判定本题考察立体拼合，即题干左图与正确选项拼合成正方体。
【题目分析】
立体拼合的解题原则为凹凸一致。观察题干左图，发现外侧斜坡和其内侧上方凸出的小矩形在同一侧，而A、C两项外侧斜坡和凹进去的小矩形不在同一侧，均可排除；比较B、D两项发现，二者仅在中间位置不同，题干左图中间位置存在斜坡，根据凹凸一致的原则，选项也应存在斜坡，只有B项符合。
小贴士：
立体拼合题目无需观察整体是否可以拼合，只需观察图形特殊的“凹凸”的部分，同时要多利用排除法做题。
真题示例2（2018青海）从所给的四个选项中，选择最合适的一个填入问号处，使下图中的立体图形①、②、③和④可组成一个完整的长方体：
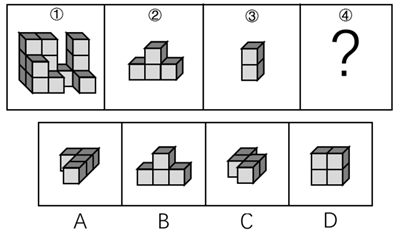
【题型判定】通过问题可直接判断题型为立体拼合，即图①②③④拼合成正方体。
【题目分析】
图①有14个小方块，图②有4个小方块，图③有2个小方块，四个选项均有4个小方块，由此可以确定图①②③④可共同构成一个4×2×3的长方体。图①方块数量最多，以其为基础根据“凹凸一致”原则进行拼接，最里面一层缺少2个小方块，可由图③填入下图蓝色位置，因图②的“凸”部分无法直接与图①的“凹”部分进行拼合，可对图②旋转或翻转，如下图所示，图②上下翻转放入黄色位置，再将C项图形立起放入橘黄色位置，即可拼成完整的正方体。故正确答案为C。
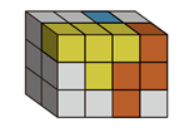
小贴士：
1.小方块立体拼合的题目近年来频繁出现，是命题的趋势，如果选项小方块数量不同，可先根据小方块的数量进行排除，如例2中若A项为5个小方块，则不可能与图①②③拼成长方体。需要强调的是此类题目看不到的位置默认是存在小方块的。
2.当选项图形与题干残缺图形无法满足“凹凸一致”的原则时，可尝试将题干图形或选项图形进行简单的旋转与翻转，再利用“凹凸一致”原则进行验证。
技巧还没掌握？扫码回复“咨询老师”
收藏此页
我要提问
